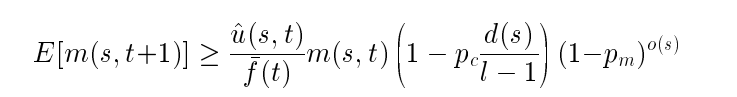
机器学习笔记一
机器学习
概念学习
ID3
ID3算法：
输入：例子集（正例、反例）；
输出：决策树
从树的根结点开始，每次都用“最好的属性”划分结点，直到所有结点只含一类例子为止。
信息增益
Gain(A)=I(p,n)-E(A)
其中，p、n是结点node的正、反例个数。A要扩展结点node的属性， pi、 ni是C 被A划分成的V个子集{C1, …Cv}的正、反例个数。
例子
例如：
属性outlook,有三个值，{sunny,overcast,rain},用outlook扩展根结点得到三个子集{C1,C2,C3}。C1={1-,2-,8-,9+,11+},C2={3+,7+,12+,13+}, C3={4+,5+,6-,10+,14-}
根结点:P=9,n=5
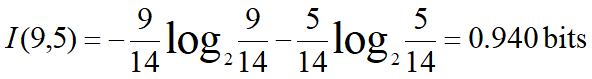
P1=2, n1=3 I(2,3)=0.971
P2=4, n2=0 I(4,0)=0
P3=3, n3=2 I(3,2)=0.971
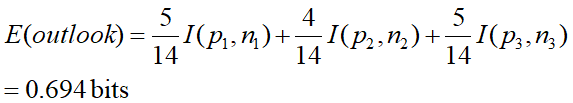
Gain(outlook)=0.940-E(outlook)=0.246bits
gain(temperature) = 0.029 bits
gain(humidity) = 0.151 bits
gain(windy) = 0.048 bits
选outlook作为根节点
分别再计算outlook值为sunny,overcast,rain的三种情况下，选谁作为叶子节点。
决策树学习的常见问题
不相关属性
属性A有v个属性值，A的第I个属性值对应Pi个正例、ni个反例。
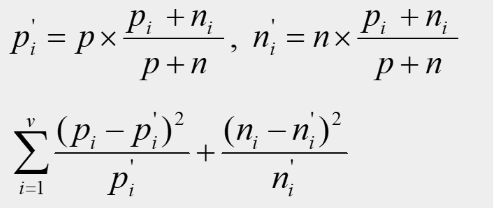
若趋近于0，则不相关
不充足属性
两类例子具有相同属性值。没有任何属性可进一步扩展决策树。哪类例子多，叶结点标为哪类。
未知属性 (贝叶斯方法)
某个例子的某个属性值缺失的情况
① “最通常值”办法 （填上出现次数最多的）
② 决策树方法: 把未知属性作为“类”，原来的类作为“属性” （根据结果倒推决策树）
③ Bayesian 方法 （算该例在正例/反例的情况下，属性值为Ai的概率 ，求最大值 ，与①的区别是考虑了 结果正例与反例的影响）
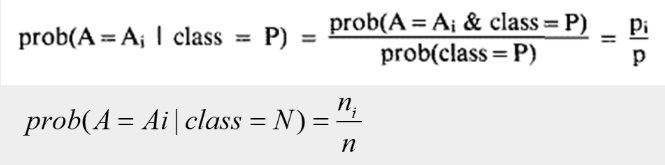
④ 按比例将未知属性值例子分配到各子集中：
属性A有v个值{A1,…,Av}, A值等于Ai的例子数pi和ni，未知属性值例子数分别为pu和nu, 在生成决策树时Ai的例子数
Pi+pu·ratioi ni+nu·ratioi
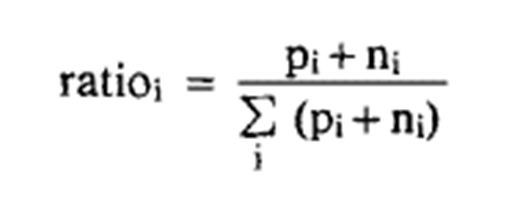
过适合
ID3算法——减枝
先生成一棵树，分别测试每个内部节点。
若把该节点下面的树剪掉，其精度是否得到改进，若改进则加入候选。
最后选择一个精度最高的内部节点，把它下面的树减去。
减去之后重复上述过程。
直到任何一个内部节点，下面的子树的精度都不改进。
减去后存在，节点中既有正例也有反例的情况。
选择粒子多的，看对应粒子集合比例，哪类粒子数量多，就把该节点标成什么。
规则学习—基本概念
定义1 （例子）. 设E=D1×D2 ×… ×Dn 是n维有穷向量空间，其中 Dj是有穷离散符号集。E中的元素e=(V1,V2, …,Vn)简记为
D1={高，矮}；D2={淡黄，红，黑}；D3={兰，褐}
E=D1 × D2 × D3
例子 e=(矮，淡黄，兰）
定义2.选择子是形为[xj=Aj]的关系语句，其中xj为第j个属性，Aj Dj; 公式（或项）是选择子的合取式，即 [xj=Aj], 其中 J {1, …,n}; 规则是公式的析取式，即 ，其中Li为公式。
一个例子e=<V1, …Vn>满足选择子（公式、规则）的条件也称做选择子（公式、规则）覆盖该例子。
例如： 例子e=<矮，淡黄，兰> 满足选择子[头发=淡黄∨红色]和 [眼睛=蓝色] ；满足公式[头发=淡黄∨红色] [眼睛=蓝色] 。
定义3：普化(generalize) :减少规则的约束，使其覆盖更多的训练例子叫普化。
定义4：特化(specialize) : 增加规则的约束，使其覆盖训练例子较少叫特化。
定义5：一致：只覆盖正例不覆盖反例的规则被称为是一致的。
定义6：完备：覆盖所有正例的规则被称为是完备的。
GS
输入： 例子集；
输出： 规则；
原则： (a) 从所有属性值中选出覆盖正例最多的属性值；
(b) 在覆盖正例数相同的情况下，优先选择覆盖反例少的属性值；
设PE,NE是正例，反例的集合。 PE’,NE’是临时正，反例集。CPX表示公式，F表示规则（概念描述）。
- F←false;
- PE’ ←PE, NE’ ←NE, CPX←true;
- 按上述(a) (b)两原则选出一个属性值V 0 , 设V 0 为第j0个属性的取值，CPX←CPX∧ [Xj0=V0]
- PE’ ← CPX覆盖的正例，NE’ ← CPX覆盖的反例，如果NE’不为空，转(3);
否则，继续执行(5);
(5) PE←PE\PE’, F ←F ∨CPX, 如果PE= ⵁ ,停止，否则转(2);
例子
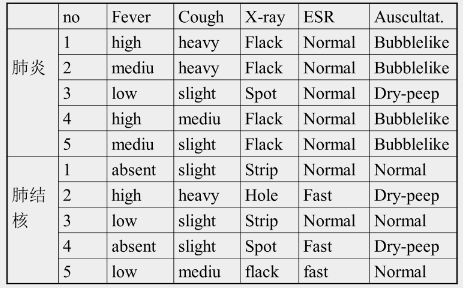
学习结果
[ESR=normal][Ausculation=bublelike] ∨[X-ray=spot][ESR=normal] => 肺炎
AQ
输入：例子集、参数#SOL、#CONS、Star的容量m、优化标准；
输出：规则；
一致：只覆盖正例不覆盖反例的规则被称为是一致的。
完备：覆盖所有正例的规则被称为是完备的。
1）Pos和NEG分别代表正例和反例的集合
① 从Pos中随机地选择一例子
② 生成例子e相对于反例集NEG的一个约束Star(reduced star),
G(e|NEG,m) , 其中元素不多于m个。
③ 在得到的star中，根据设定的优化标准LEF找出一个最优的公式D。
④ 若公式D完全覆盖集合Pos,则转⑥
⑤ 否则，减少Pos的元素使其只包含不被D覆盖的例子。从步骤①开始重复整个过程。
⑥ 生成所有公式D的析取，它是一个完备且一致的概念描述。
- Star生成: Induce方法
①例子e的各个选择符被放入PS(partial star)中,将ps中的元素按照各种标准排序.
②在ps中保留最优的m个选择符.
③对ps中的选择符进行完备性和一致性检查,从ps中取出完备一致的描述放入SOLUTION表中,若SOLUTION表的大小大于等于参数#SOL,则转⑤.
一致但不完备的描述从ps中取出放入表CONSISTENT中,若CONSISTENT表的大小大于等于参数#COS,则转⑤;
④对每个表达式进行特殊化处理,所有得到的表达式根据优化标准排列,仅保留m个最优的.重复步骤③，④.
⑤得到的一般化描述按优先标准排序,保留m个最优的表达式构成约束Star(e|NEG,m).
例子
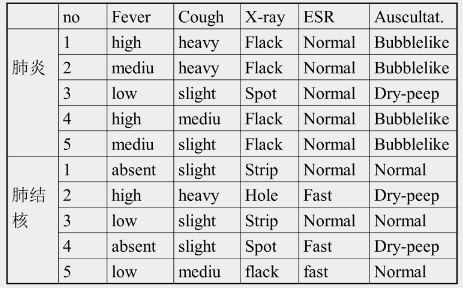
#SOL=2
#CONS=2
M=2
优化标准: 正例数/反例数
种子 e1+: [Fever=high][Cough=heavy][X-ray=flack][ESR=normal][Auscultation=bubblelike]
第一轮:
（进入Induce算法）
Ps:
⑤ [Fever=high] <2,1>
④[Cough=heavy] <2,1>
②[X-ray=flack] <4,1>
③[ESR=normal] <5,2>
①[Ausculation=bubblelike] <4,0>
保留m个表达式
[Auscultation=bubblelike] 一致的表达式,放入CONSISTENT中
[X-ray=flack] 特化;
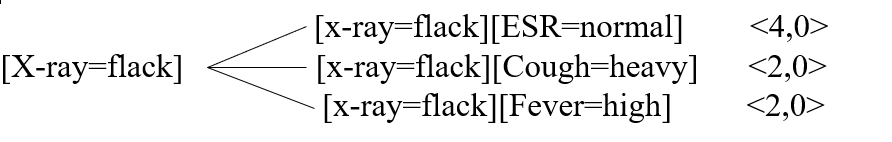
保留2个表达式，2个表达式均为一致的,放入CONSISTENT中,按优先标准排序CONSISTENT中表达式,保留m(2)个表达式.
[Ausculation=bubblelike]
[x-ray=flack][ESR=normal]
（出Induce算法）
选出一个最优的作为D
D: [Auscultation=bubblelike]
将D覆盖的正例去掉. 去掉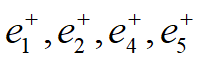
第一轮结束.
第二轮:
种子 e3+: [Fever=low][Cough=slight][x-ray=spot][ESR=normal][Auscultation=dry-peep]
Ps:
④[fever=low] <1,2>
⑤[Cough=slight] <1,3>
①[x-ray=spot] <1,1>
②[ESR=normal] <1,2>
③[Ausculation=dry-peep] <1,2>
保留m(2)个表达式:
[ESR=normal]
[x-ray=spot]
特殊化:
保留m(2)个表达式
[x-ray=spot] [ESR=normal]
[x-ray=spot] [fever=low]
上面2个表达式都是一致的,放入CONSISTENT表中,按优先标准排序,并选出一个最优的作为D
D: [x-ray=spot] [ESR=normal]
将D覆盖的正例从pos中去掉,去掉 e3+ ,pos空.
生成规则:
[Ausculation=bubblelike] v [x-ray=spot] [ESR=normal] => 肺炎
算法结束.
扩张矩阵算法
表2.7正例矩阵与反例矩阵
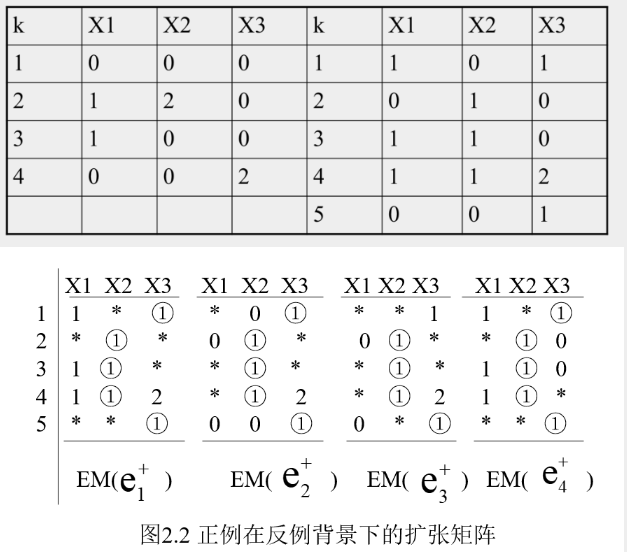
定义2: 在一个扩张矩阵中，由分别来自不同行的m个非死元素连接组成它的一条路（径）；在两个以上的扩张矩阵中，具有相同值的对应的非死元素叫做它们的公共元素；在两个或两个以上扩张矩阵中出现的路叫公共路；具有公共路的两个扩张矩阵叫做相交的，否则叫做不相交的。
扩张矩阵里的一条路就对应一个公式，这个公式覆盖了正例，排除了所有反例。
注意只要选到路径里的元素，对应属性就不等于它。
比如 1 不选到路径里，就是 X2 不等于1，注意这对应X2，这两个 1 选进去了，这是对应X3，所以这就是 X3 不等于1。元素只要选择路径不等于它。
X2 不等于1。假设值域是 0- 2，所以我们就假定它值域是 0- 2， X2 不等于1， X2 等于， 0 或者2。
X3 不等于1，也是 X3 等于 0 或者2。
找尽量少的公告路径，路径条数越少越好
AE1
优先选择“最大公共元素”来形成路径，即在最多数目的扩张矩阵中出现的元素。
第一行中红圈的1在四个扩张矩阵中都出现过，则先该元素。第二行同理。
广义扩张矩阵
广义扩张矩阵就是用公式对反例做扩张矩阵
定理2.1 公式L覆盖公式A又覆盖公式B，当且仅当它覆盖A ⚪+ B。
定理2.2 一个例子集合被一个一致的规则所覆盖，则这些例子的合并也是一致的。
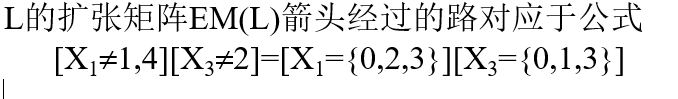
FIND-S
每个数据对象都代表一个概念和假设。我们认为这样的一个假设 <true，true，false，false> 是更具体的，因为它只覆盖了一个实例。一般来说，我们可以在这个假设中加入一些符号。我们有以下符号：
ⵁ （一个拒绝所有实例的假设）
< ? , ? , ? , ? > （全部接受）
<true, false, ? , ? >（部分接受）
- 将 h 初始化为 H 中最特殊假设
- 对每个
正例 x
• 如果 h(x)≠c(x)，则用覆盖 x 的 h 的极小普化式替代 h - 输出假设 h
Find-S 算法的局限性
用于概念学习的 Find-S 算法是机器学习最基本的算法之一，但它也具有如下的不足和缺点：
- 没有办法确定最终假设（Find-S 找出的）是否是唯一一个与数据一致 (consistent) 的假设。
- 不一致 (inconsistent) 的训练实例会误导 Find-S 算法，因为它忽略了 “负” 数据实例。一个能检测训练数据不一致的算法是更好的选择。
- 一个好的概念学习算法应该能够回溯对找到的假设的选择，以便能够逐步改进所得到的假设。但不幸的是，Find-S 不能提供这样的方法。
候选消除算法
候选消除算法它能解决FIND-S中的若干不足之处。其输出的是与训练样例一致的所有假设的集合。
候选消除算法的目的是引入若干基本的机器学习问题提供一个良好的概念框架。
首先将G边界和S边界分别初始化为H中最一般的假设和最特殊的假设。即:
【正例使得变型空间的S边界逐渐一般化，而反例扮演的角色恰好使得G边界逐渐特殊化。每输入一个训
练样例，S和G边界将继续单调移动并相互靠近，划分出越来越小的变型空间。】
候选消除算法
将 G 集合初始化为 H 中极大一般假设 {< ?, ?, ?, ?, ?, ? >}
将 S 集合初始化为 H 中极大特殊假设 {<Φ, Φ, Φ, Φ, Φ, Φ>}
对每个训练样例 d，进行以下操作：（使得S被一般化，G被特殊化）
- 如果 d 是一正例
- 从 G 中移去所有与 d 不一致的假设
- 对 S 中每个与 d 不一致的假设 s
- 从 S 中移去 s
- 把 s 的所有的极小泛化式 h 加入到 S 中，其中 h 满足
- h 与 d 一致，而且 G 的某个成员比 h 更一般
- 从 S 中移去所有这样的假设：它比 S 中另一假设更一般
- 如果 d 是一反例
- 从 S 中移去所有与 d 不一致的假设
- 对 G 中每个与 d 不一致的假设 g
- 从 G 中移去 g
- 把 g 的所有的极小特殊化式 h 加入到 G 中，其中h 满足
- h 与 d 一致，而且 S 的某个成员比 h 更特殊
- 从 G 中移去所有这样的假设：它比 G 中另一假设更特殊
例子
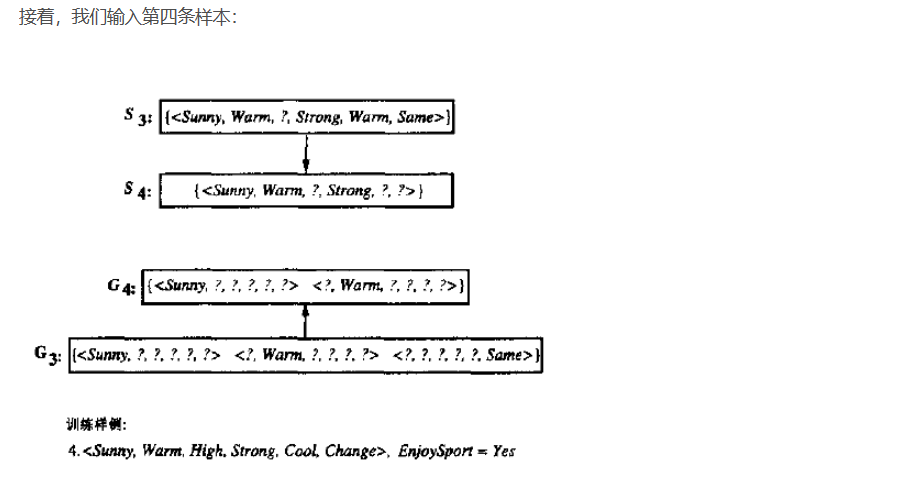
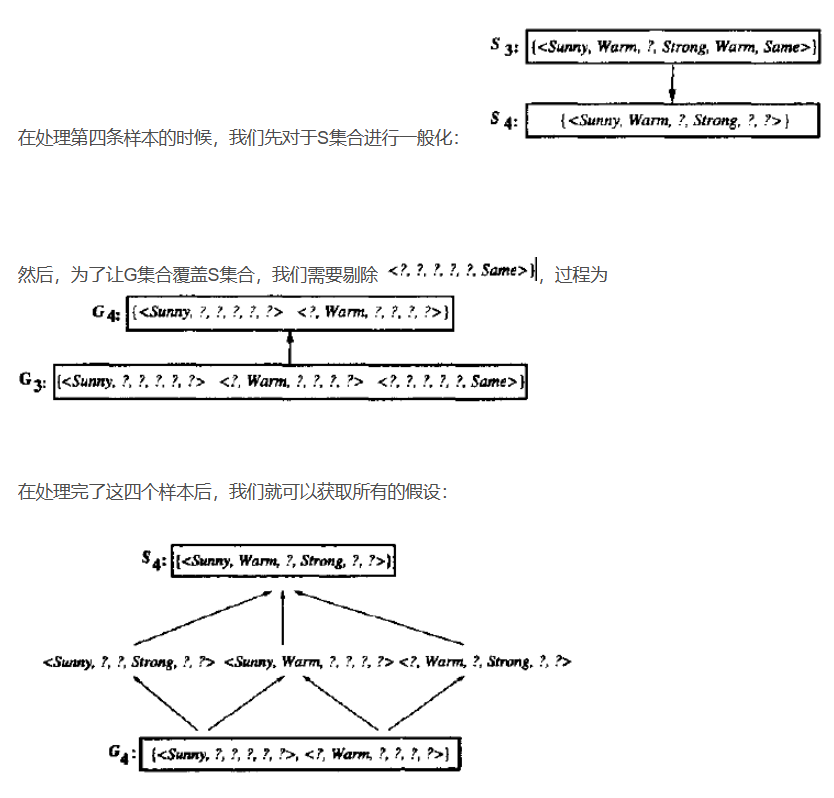
局限性
1.对噪点兼容性非常差
2.当我们某个属性有10+个值的时候，往往这个属性必然被一般化，所以我们需要对数据进行预处理
神经网络
神经网络的学习算法就是要得到一组合适的权值。
人 工神经网络重点在于自动的调节权值
什么时候用神经网络
第一，输入是高维的，离散的或者实数值的。
第二，输出是离散的或者是实数值的。
第三，输出是值的向量，值的向量就可以有多个值。
第四，有一定的抗噪音能力，有一定的容错性。
第五，目标函数的形式是未知的，时候使用神经网络一般都是这种情况。
第六，神经网络得到的结果的人类的可读性不重要的时候才能使用神经网络。
感知器
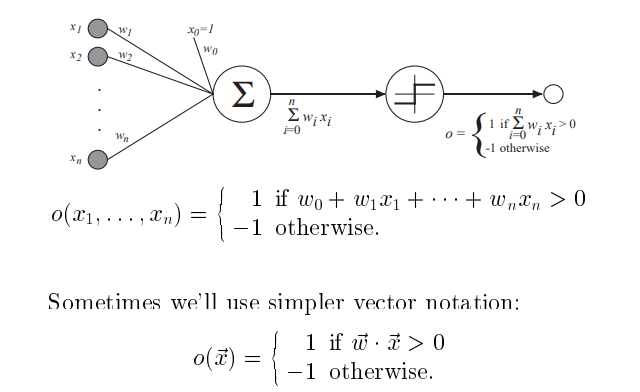
n个输入 x1-xn 即例子的属性
对应每个输入有w1-wn不同的权值。(首先随机给一组初始的权值。)
有一个x0恒为1 ， w0 为阈值。
输出为加权累加和>0 则输出1 ，否则输出 -1
根据例子数据 反复修正w权值。最后，w 值会收敛于一组合适的值
权值调节规则
t为真实输出
o是神经网络预测输出
η 是学习速率，决定调节幅度
Perceptron training rule 感知器训练规则
Can prove it will converge
可以证明它会收敛
If training data is linearly separableand n sufficiently small
如果训练数据是线性可分的，且η足够小
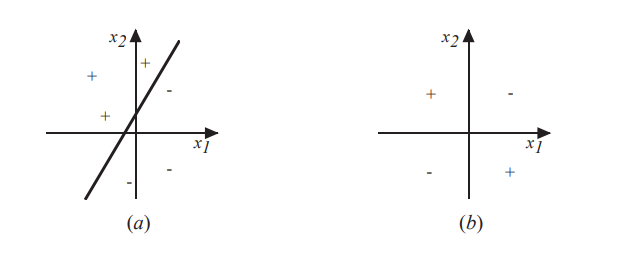
（a）是线性可分 ，（b）不是。
梯度下降算法 Gradient Descent
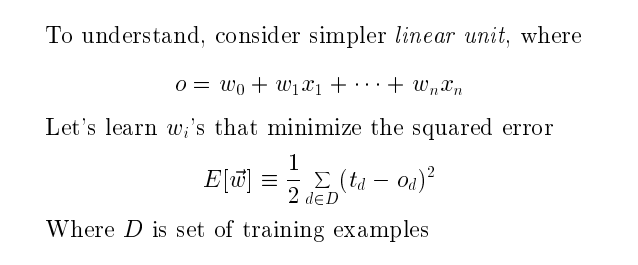
d是训练例子，D是训练例子集合
误差为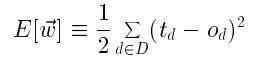
所有训练粒子真实的输出和神经网络的例子的输出误差平方和
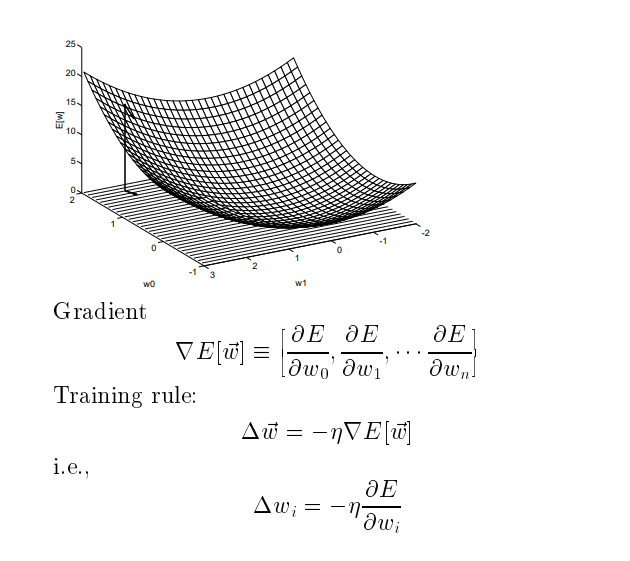
上图为只有w0和w1的误差曲面图。
梯度下降是沿梯度的反方向。
某点梯度是沿曲面向上最陡峭的方向。所以梯度的反方向就是这点向下最陡峭的方向。由于是最陡峭的方向，所以在这个点沿这个方向每下降一次，下降的幅度最大。
（贪心算法）局部最优，不能保证全局最优。
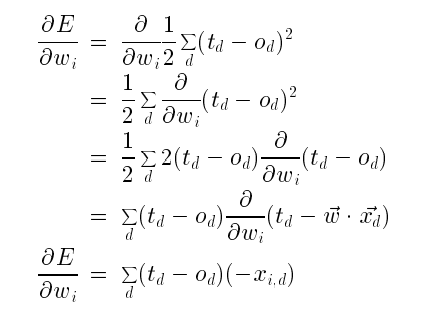
批量梯度下降算法
η足够小，保证收敛，防止振荡。
对每个例子求▲wi 的累加，再去调节wi，每次都用到了全部的例子。
随机梯度下降算法
相比批量，没有小循环，每次随机选取一个例子，得到▲wi后直接加到 wi上。
(陷入局部极小的可能性就会减小,不一定能完全克服)
小批量梯度下降算法
每次选取固定个数的例子，进行调节▲wi 。 相比批量，每次只用到固定数量的例子。
多重神经网络
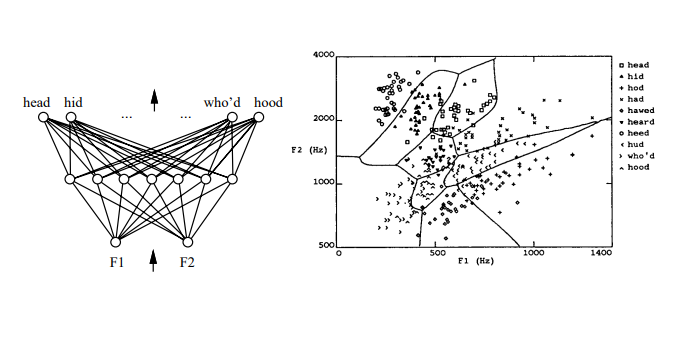
中间这层节点，隐藏节点，即其输出并不知道。
想形成这么复杂的决策区域，多成神经网络的节点不能是线性单元
多重神经网络里的节点不能用线性线性单元了，不能用加权累加了
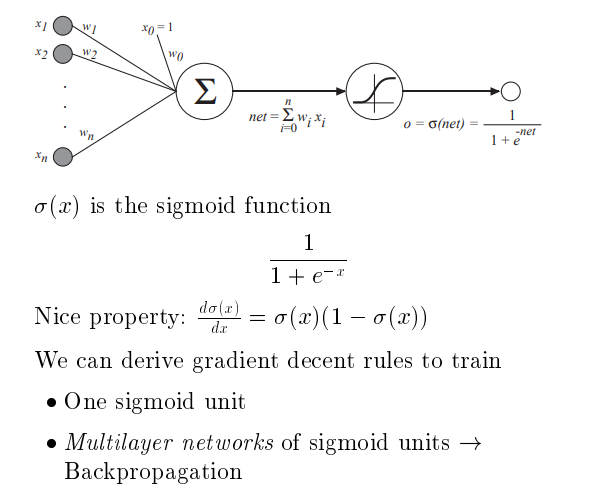
其使用Sigmoid 函数
Sigmoid Unit
只有输入不是sigmoid 单元，上图包含了两个sigmoid单元
反向传播算法
误差反向传播就是输出节点的误差，能求出来它误差往下传播。反向下面节点的误差是上一层节点的误差的加权累加和。
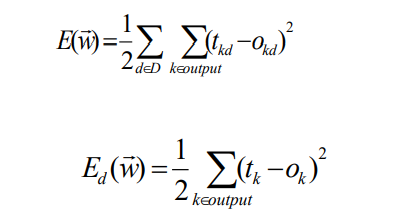
两种误差，上是所有例子产生的误差，下是随机例子产生的误差。
前馈网络，是值往前传。
克服局部最小
-
给一个冲量
-
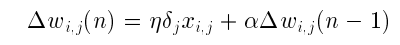
随机梯度下降
-
用不同的初始权值多次训练神经网络
过适合处理方式
K交叉
假设我有 m 个训练例子，我把这 m 个训练个例子分成 k 份，分成 k 分，当然每份就是 m 除 k 了。假定它是整数，分成 k 分。
每次拿出一份做预测，用测预测精度，其他 k 减 1 份。我训练神经网络权值。
把第二份再拿出来，就拿第二份，剩下 k 减 1 份训练神经网络拿出来这份做预测，所以我得到第二个次数，每一份都拿出来做预测，剩下那些做训练，得到 k 个次数。
把这 k 个次数求一个平均值，这个平均值就是神经网络训练神经网络合适的次数
遗传算法
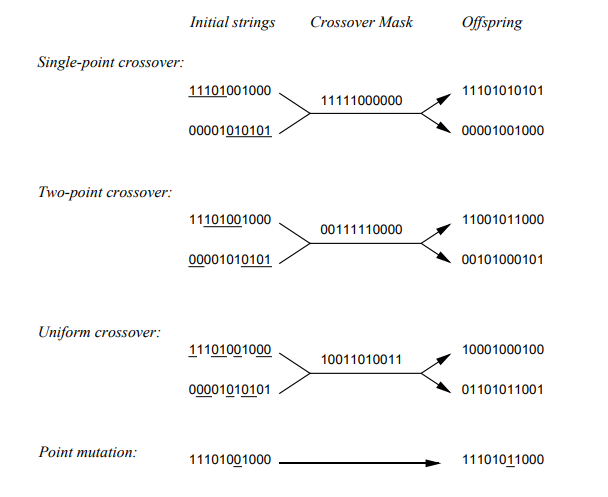
Crossover Mask 交叉点
单点交叉
两点交叉
均匀交叉：均匀交叉涉及多个点，每个交叉点这个是随机选，所以被选到的概率是等概率的。
变异
编码方案
例如Outlook有三个属性值Sunny、Overcast、Rain
三个属性值用三位数表示。
000都不取，111都可以取。
001 Outlook = Rain
010 Outlook = Overcast
100 Outlook = Sunny
011 Outlook = Rain v Overcast ...
遗传算法原型
P是当前一代，
Ps是下一代。
在选择中 ，概率的方法 相当于轮盘赌。
这个轮盘分很多扇区，不同的扇区，分一些扇区轮盘转，有一个小球在轮盘上也转，比如轮盘一般顺时针转，小球一扔，好像逆时诊断在轮盘里。最后轮盘停了，小球也会停。如果小球停到哪个扇区了？如果你压这个山区了，你就赢了。你没压这个山区，你就输了。
轮盘赌例子
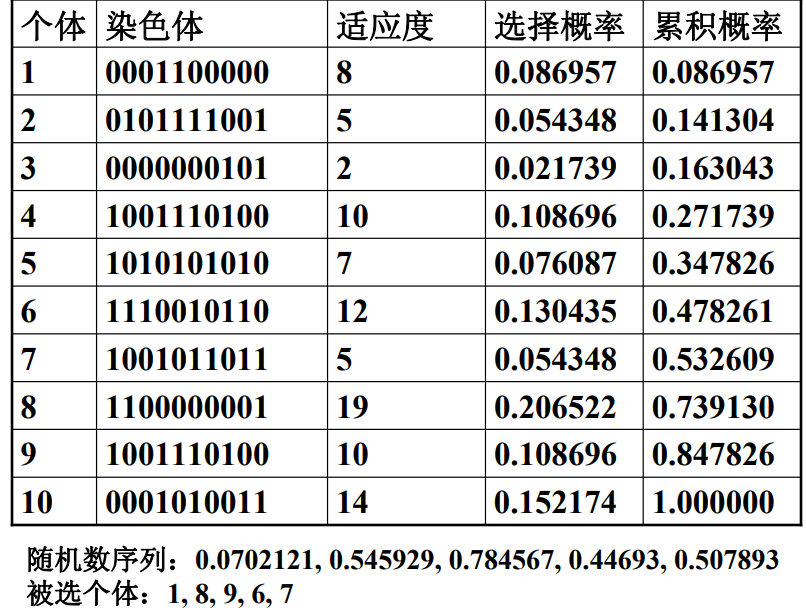
被选到的个体，可以重复。
局限性—拥挤现象
好的基因串或者是类似的基因串，它适应度高，所以他被选的可能性大，选到的可能性大。选来选去到后面基本都是类似的基因串。
这样的基因串，它适应度高，所以它被遗传下去的可能性就大。所以经过了一些待遇之后，总群里基本都是这样。类似的基因串。总群里基因串很类似
解决：
锦标赛方法：首先随机的选出来两个假设。随机的选出两个假设之后，用概率 p 他俩再比一下，就对 H1 和 H2 他俩比较一下。对好的假设用概有一定的是概率 p 选好的假设。
当然不好的一个假设被选到的概率就是 1 减 p 了。当然 p 应该是大于 1 减 p 的，因为好的假设被选到的概率是p，如果 p 小于 1 减p，每次坏的被选到的可能性大概这种方法。
因为一开始是随机选，所以所谓的不好的基因也有机会被选到。这样多样化保持进化过程中。
排队选择法：首先根据假设的适应度给它排个序，当然，适用度差的排到前面，适用度好的排在后面。按升序排，假设被选到的概率是正比于它的排列位置，越往后选到的可能性越大。当然也可以降序排，降序排就是。当然不能是正比，得是反比。排到前面可能必须要概率大。
模式定理
模式： S1= * 1 * * * * 0 ，其中 1 和 0叫确定位
求下一代符合模式S的期望
选择步
- -f(t) 是平均适应度
- m(s,t) 模式S实例的数量
- u^(s,t) 是模式S实例的平均适应度
选择步概率
其中进行了n次独立选择 ↑
交叉步与变异步：
- 其中d(S) 是最远的两个确定位之间的距离（空的个数） d(S1)=5 (1和0之间空的个数)
- L是总的空的个数 S1的L为7
最后总的期望
