机器学习2

消极学习与积极学习

积极学习(Eager Learning)
这种学习方式是指在进行某种判断（例如，确定一个点的分类或者回归中确定某个点对应的函数值）之前，先利用训练数据进行训练得到一个目标函数，待需要时就只利用训练好的函数进行决策，显然这是一种一劳永逸的方法，SVM就属于这种学习方式。
消极学习(Lazy Learning)
这种学习方式指不是根据样本建立一般化的目标函数并确定其参数，而是简单地把训练样本存储起来，直到需要分类新的实例时才分析其与所存储样例的关系，据此确定新实例的目标函数值。也就是说这种学习方式只有到了需要决策时才会利用已有数据进行决策，而在这之前不会经历 Eager Learning所拥有的训练过程。KNN就属于这种学习方式。
比较
• Eager Learning考虑到了所有训练样本，说明它是一个全局的近似，虽然它需要耗费训练时间，但它的决策时间基本为0.
• Lazy Learning在决策时虽然需要计算所有样本与查询点的距离，但是在真正做决策时却只用了局部的几个训练数据，所以它是一个局部的近似，然而虽然不需要训练，它的复杂度还是需要 O(n),n 是训练样本的个数。由于每次决策都需要与每一个训练样本求距离，这引出了Lazy Learning的缺点：(1)需要的存储空间比较大 (2)决策过程比较慢。
典型算法
• 积极学习方法:SVM;Find-S算法;候选消除算法;决策树;人工神经网络;贝叶斯方法;
• 消极学习方法:KNN;局部加权回归;基于案例的推理;

FOIL算法

rule set R={ }
外循环(P不为空)
- N'=N , P'=P , r={}
- 内循环执行while(当N’为空，或r长度大于最大长度时)：
  - 计算出每个属性值的增益，选出最大的那个。（例如，age<=30)
  - 将该属性值加入规则r中 (例如,r={age<=30,...})
    - 移除P’、N'中不满足规则r的元组
  - 当N’为空，或r长度大于最大长度时，跳出内循环
- R=RU
- 移除p中满足r的元组
return R

概率意义下的机器学习

KNN-K近邻算法

欧氏距离度量

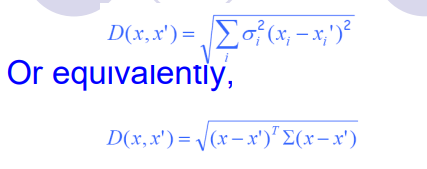
k 值的选择

不同k值的影响
一般而言，从k = 1开始，随着的逐渐增大，K近邻算法的分类效果会逐渐提升；在增大到某个值后，随着的进一步增大，K近邻算法的分类效果会逐渐下降。

特例：k = 1（最近邻算法）
此时，KNN的泛化错误率上界为贝叶斯最优分类器错误率的两倍（证明见最后）

特例：k = N
K近邻算法对每一个测试样本的预测结果将会变成一样（属于训练样例中最多的类）。

k值选择
一般k值较小。
k通常取奇数，避免产生相等占比的情况。
往往需要通过交叉验证(Cross Validation)等方法评估模型在不同取值下的性能，进而确定具体问题的K值。

分类决策规则

一般都是多数表决规则(majority voting rule)，即把k个邻近的多数类别作为测试样本的类别

算法流程

总体来说，KNN分类算法包括以下4个步骤：
①准备数据，对数据进行预处理。
②计算待分类点到其他每个样本点的距离。
③对每个距离进行排序，然后选择出距离最小的K个点 。
④对K个点所属的类别进行比较，根据少数服从多数的原则，将测试样本点归入在K个点中占比最高的那一类。

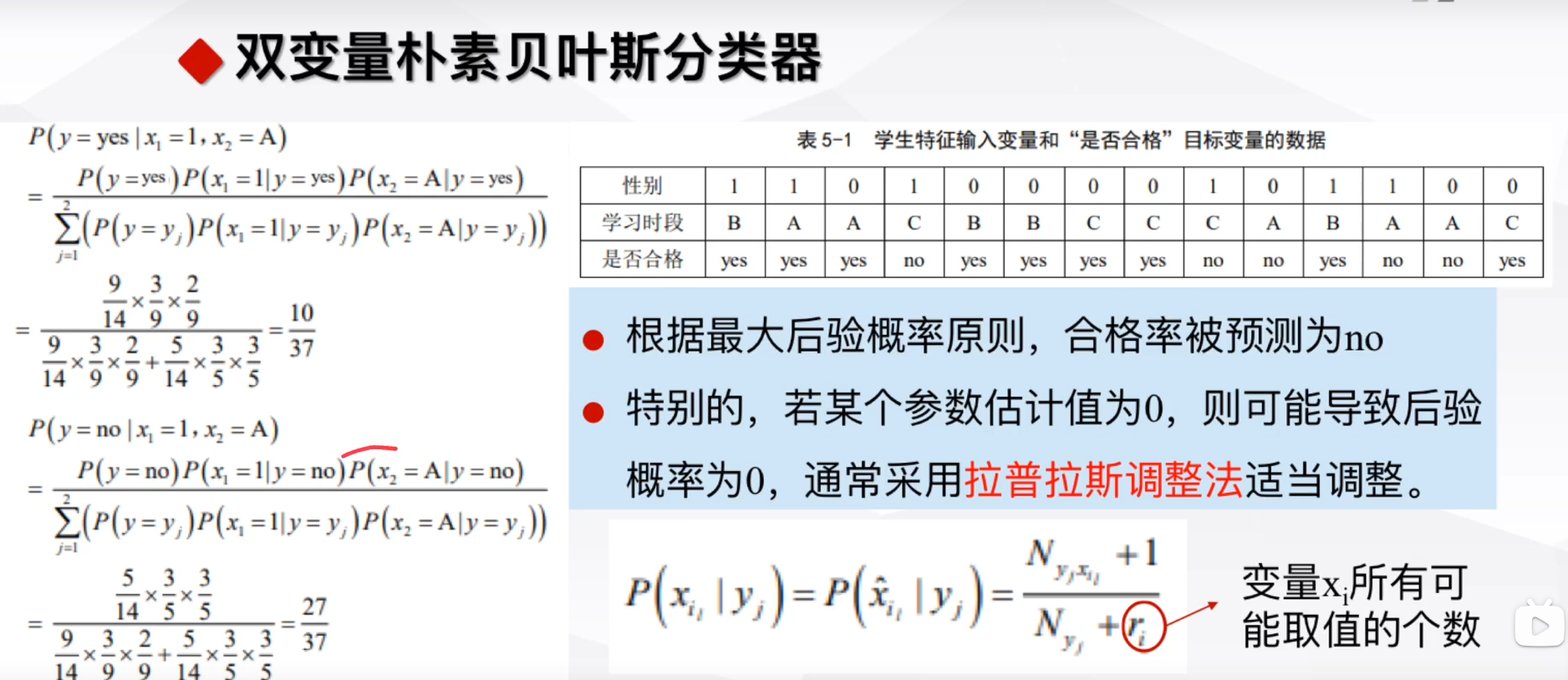
贝叶斯分类器

目标求后验概率P(Y|X)
用到先验概率P(Y)与条件概率P(X|Y)

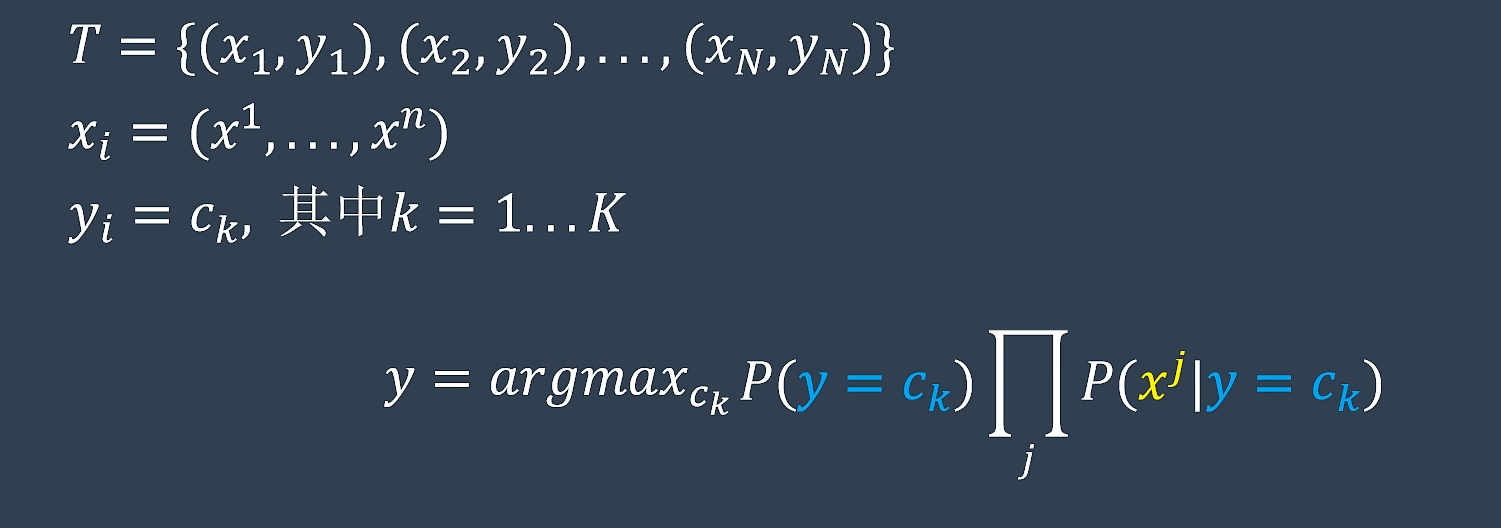
贝叶斯最优分类器

新实例的最可能分类可通过合并所有假设的预测得到,用后验概率来加权。如

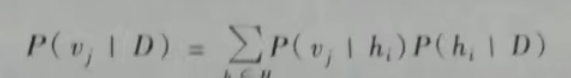
线性回归

线性回归做预测，让一条线尽可能通过更多的点

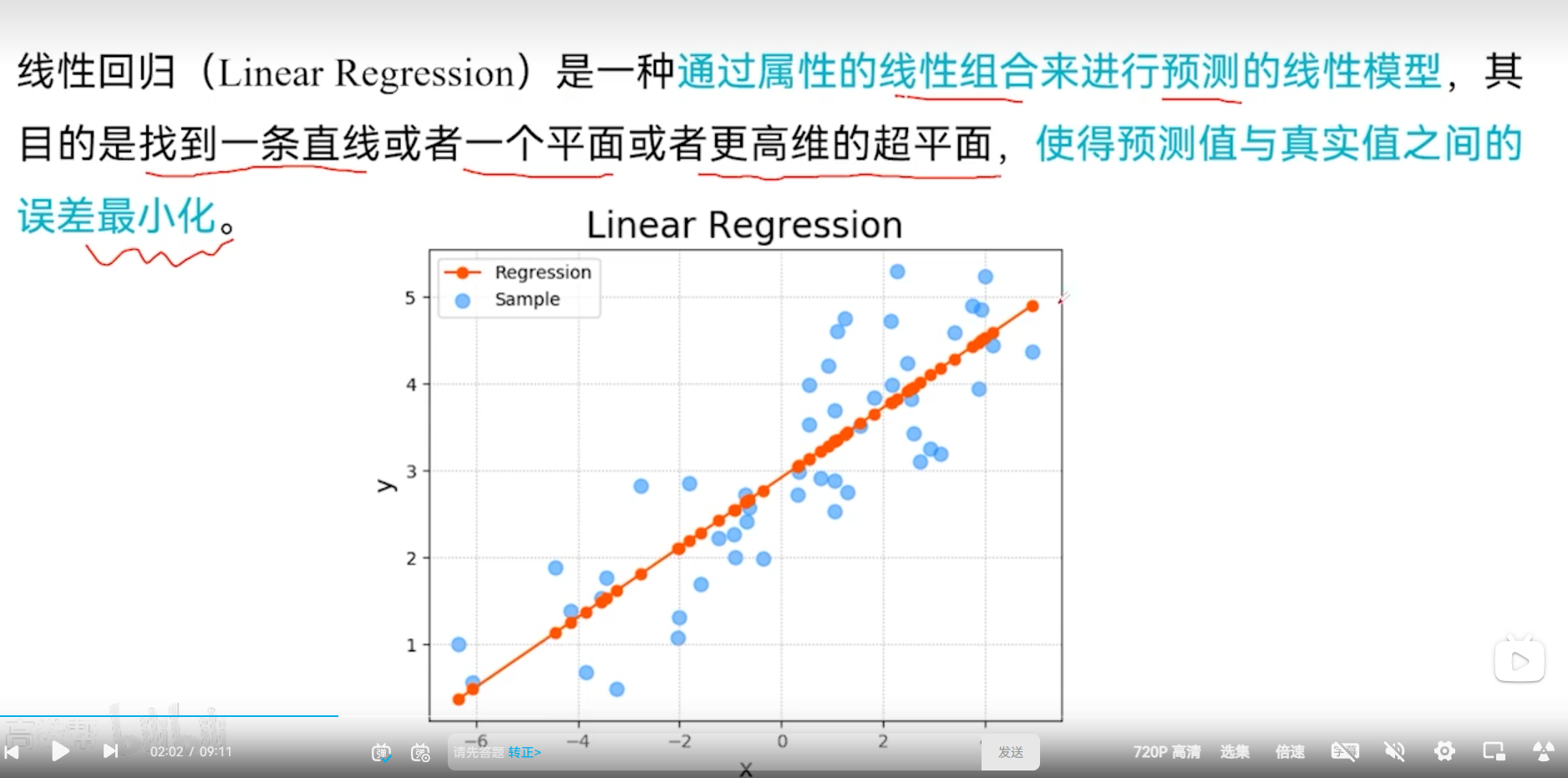
逻辑回归

利用逻辑回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式

优点：
以概率的形式进行输出，而非0或1的判定。
简单高效，计算速度快，易于理解和实现，易并行，在大规模数据情况下非常适用
直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确所带来的问题;

缺点：
逻辑回归对共线性非常敏感，x1=ax2+bx3
容易欠拟合，
本质上是线性分类器，处理不好特征之间相关的情况

逻辑回归主要基于以下三个目的:
(1)预测结果等于1(即坏样本)的概率;
(2)对结果或预测进行分类;
(3)评估模型预测的相关概率或风险。

逻辑回归原理——构造函数

Sigmoid函数
因此我们需要构造一个函数，将(一oo,+ oo)内的实数值变换到区间(0,1)上。
构造函数如下:

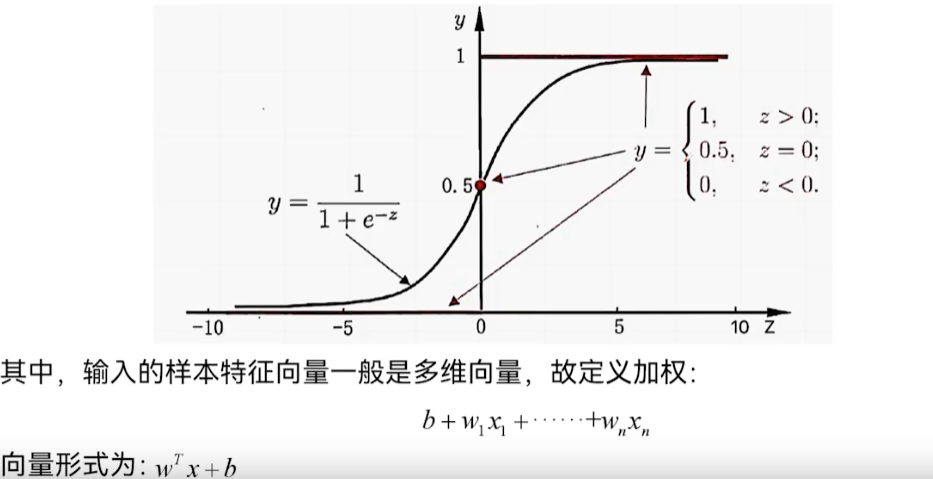
设置分布函数

分类规则

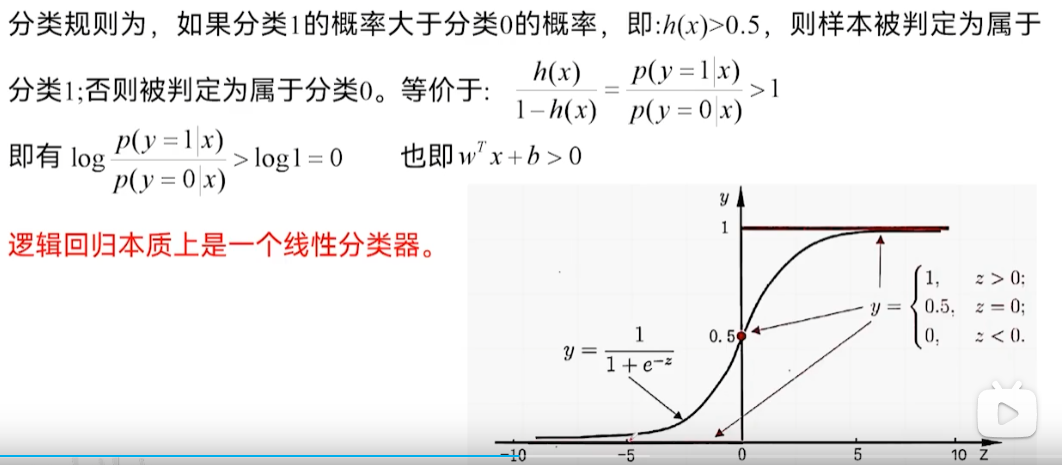
最佳回归系数确定

w与b的系数
梯度下降法

SVM

SVM视频

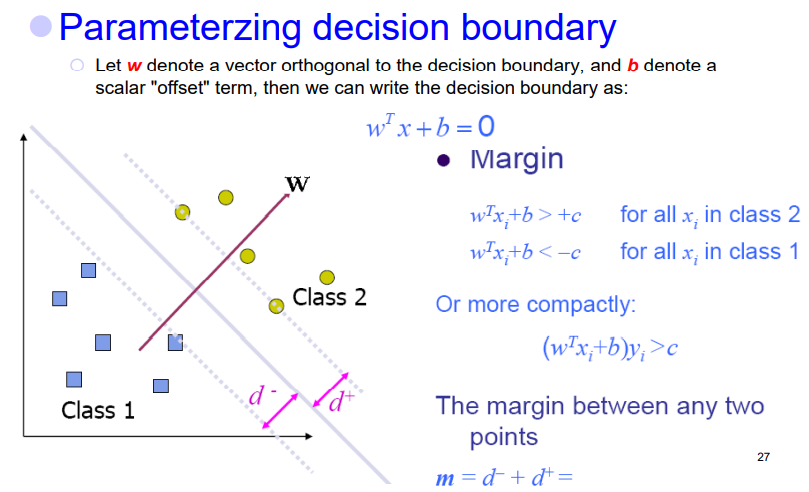
求最大Margin

“最小”允许margin为：

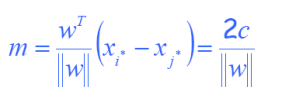
这是我们的最大margin分类问题：

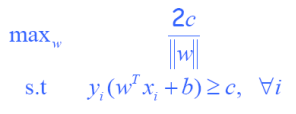
软间隔

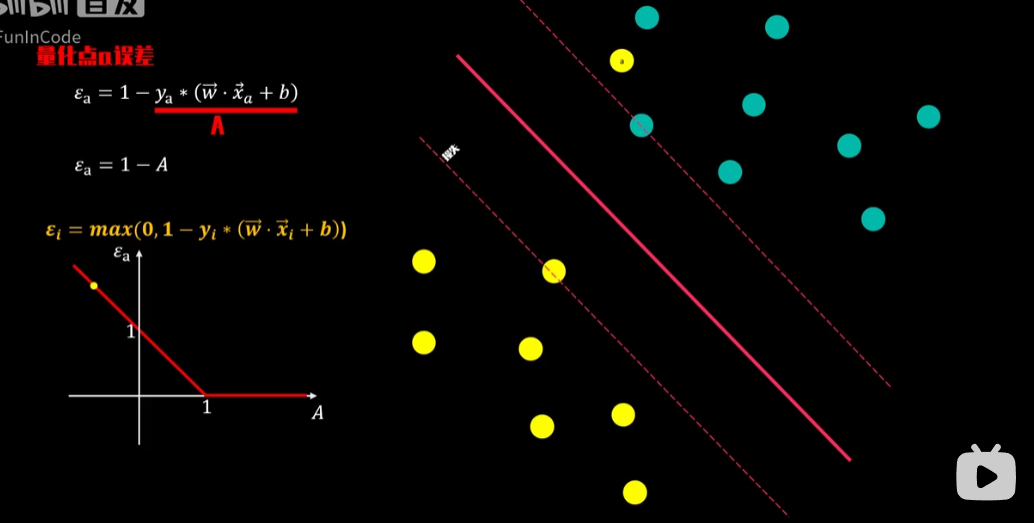
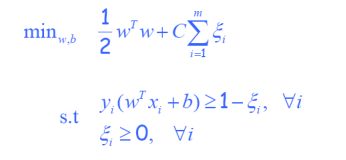
ξi是优化中的“松弛变量”
注意，如果xi没有误差，ξi=0

ξi是错误数的上限
C：误差和裕度之间的权衡参数

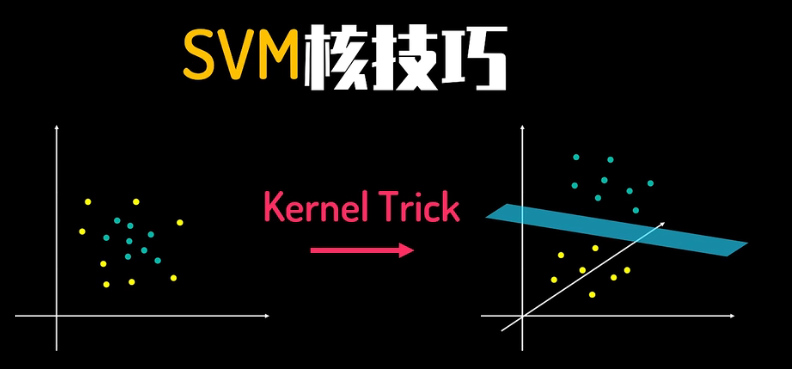
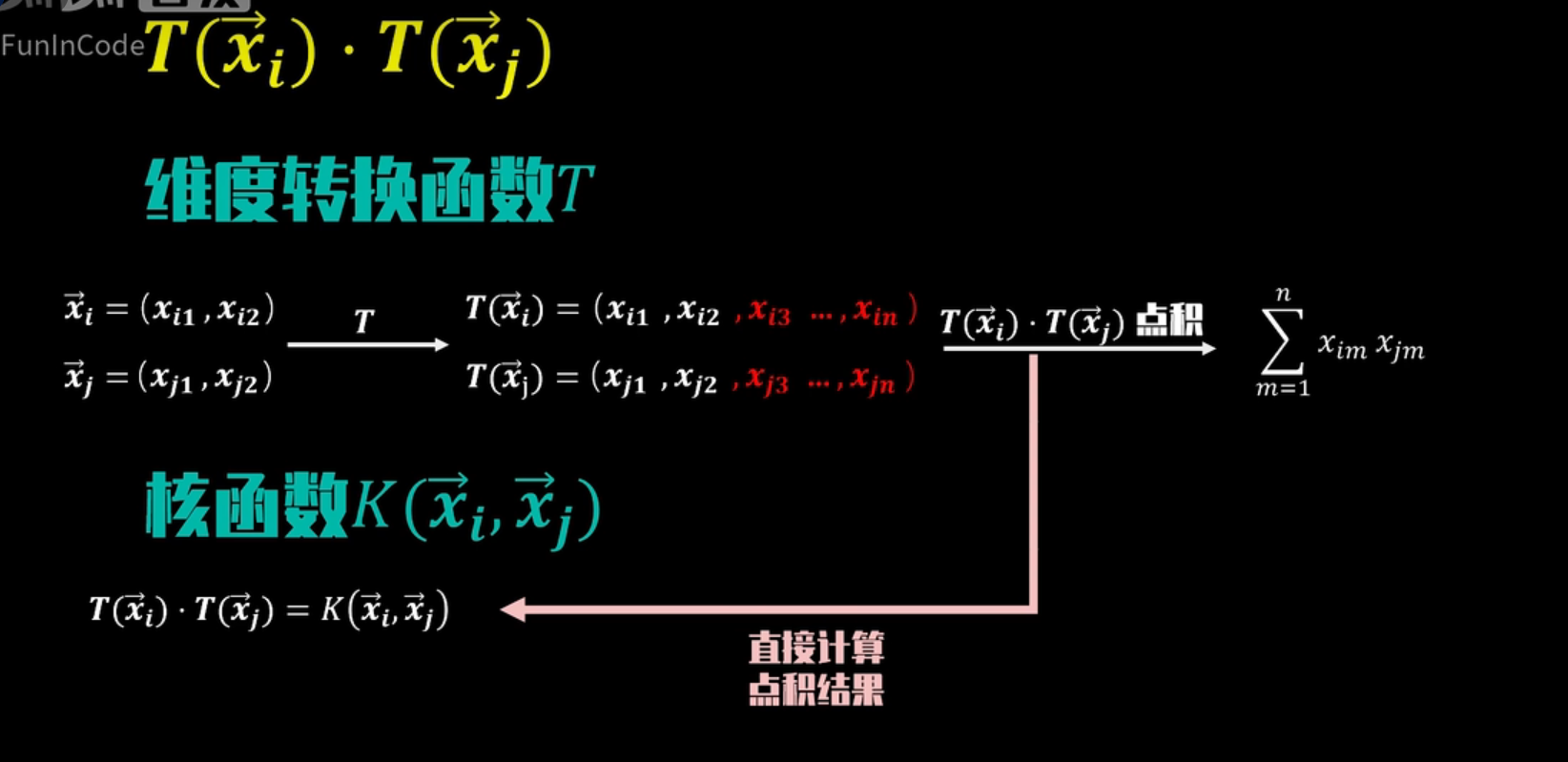
核技巧The Kernel Trick

聚类、高斯混合模型和EM算法

层次聚类

自上而下
自下而上
两两结合

K-means算法

Kmeans 基于密度

算法步骤

先定义总共有多少个类/簇(cluster)
将每个簇心(cluster centers）随机定在一个点上·将每个数据点关联到最近簇中心所属的簇上
对于每一个簇找到其所有关联点的中心点(取每一个点坐标的平均值)
将上述点变为新的簇心
不停重复，直到每个簇所拥有的点不变

计算复杂度

每次迭代时，计算n个对象与集群中心之间的距离为O(Kn)
计算质心，每个对象都会被添加一次O(N)
假设对于I迭代，这两个步骤每完成一次：O(LKN)

种子选取

结果可能因随机种子选择而异。
某些种子会导致收敛速度变差，或者收敛到次优聚类。

使用启发式方法选择好种子
尝试多个起点（非常重要！！！）
使用另一个方法的结果初始化。

有多少个集群？

给出了簇数K
将n个对象划分为预定数量的簇
找到“正确”数量的集群是问题的一部分
给定对象，将其划分为“适当”数量的子集。
解决优化问题：惩罚拥有大量集群
依赖于应用，例如搜索结果列表的压缩摘要。
信息论方法：基于模型的方法
在拥有更多集群（更好地集中于每个集群）之间进行权衡集群），并且集群太多
非参数方法–让集群数量随数据点/对象的数量

高斯混合模型GMM

基于模型的聚类
与基于划分的聚类和基于密度的聚类不同，基于模型的聚类采用概率模型来表达聚类原型。
基于模型的方法假设数据集是由一系列的概率分布所决定的，给每一个聚簇假定了一个模型，然后在数据集中寻找能够很好满足这个模型的簇。
GMM首先随机生成正态分布的参数：如均值和方差是多少，其中E步为计算每个样例属于第几个高斯分布的概率，选择概率大的作为其所在分布。根据被分到不同高斯分布的n个例子结果，重新估计每个高斯分布的参数，属于M步。

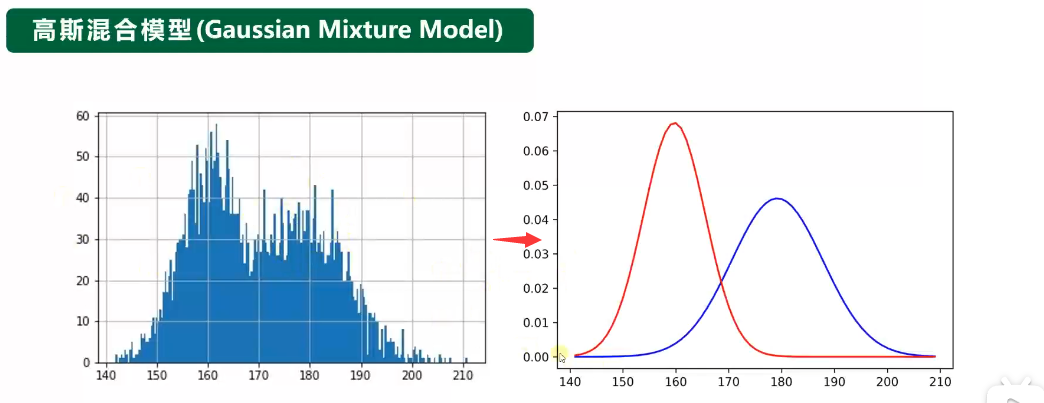
GMM是一种聚类算法，是多个高斯分布函数的线性组合，用于解决同一集合下的数据包含多种不同分布的情况。
GMM是指具有以下形式的概率分布模型：

EM算法

Expectation-Maximization (EM) 期望最大化
EM算法是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，
其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation Maximization Algorithm）

EM算法优缺点以及应用

优点：简介中已有介绍，这里不再赘述。
缺点：对初始值敏感：EM算法需要初始化参数θ，而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
EM算法的应用：
- k-means算法是EM算法思想的体现，E步骤为聚类过程，M步骤为更新类簇中心。
- GMM（高斯混合模型）也是EM算法的一个应用，GMM首先随机生成正态分布的参数：如均值和方差是多少，其中E步为计算每个样例属于第几个高斯分布的概率，选择概率大的作为其所在分布。根据被分到不同高斯分布的n个例子结果，重新估计每个高斯分布的参数，属于M步。

GMM与KMeans比较

1）从上面的分析中我们可以看到 GMM 和 K-means 的迭代求解法其实非常相似（都可以追溯到 EM 算法，下一次会详细介绍），因此也有和 K-means 同样的问题──并不能保证总是能取到全局最优，如果运气比较差，取到不好的初始值，就有可能得到很差的结果。对于 K-means 的情况，我们通常是重复一定次数然后取最好的结果，不过 GMM 每一次迭代的计算量比 K-means 要大许多，一个更流行的做法是先用 K-means （已经重复并取最优值了）得到一个粗略的结果，然后将其作为初值（只要将 K-means 所得的 centroids 传入 gmm 函数即可），再用 GMM 进行细致迭代。

2)k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了，而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率，又称作 soft assignment 。

相同点
都是迭代执行的算法，且迭代的策略也相同：算法开始执行时先对需要计算的参数赋初值，然后交替执行两个步骤，一个步骤是对数据的估计（k-means是估计每个点所属簇；GMM是计算隐含变量的期望；）;第二步是用上一步算出的估计值重新计算参数值，更新目标参数（k-means是计算簇心位置；GMM是计算各个高斯分布的中心位置和协方差矩阵）
不同点
1）需要计算的参数不同：k-means是簇心位置；GMM是各个高斯分布的参数
2）计算目标参数的方法不同：k-means是计算当前簇中所有元素的位置的均值；GMM是基于概率的算法，是通过计算似然函数的最大值实现分布参数的求解的。

举例

https://blog.csdn.net/pipisorry/article/details/42550815
高斯混合模型
再回到例子本身，如果没有“男的左边，女的右边，其他的站中间！”这个步骤，或者说我抽到这200个人都戴了面具。那现在这200个人已经混到一起了，这时候，你从这200个人（的身高）里面随便给我指一个人（的身高），我都无法确定这个人（的身高）是男生（的身高）还是女生（的身高）。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？只有当我们知道了哪些人属于同一个高斯分布的时候，我们才能够对这个分布的参数作出靠谱的预测。只有当我们对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些人属于第一个分布，那些人属于第二个分布。

  为了解决这个你依赖我，我依赖你的循环依赖问题，总得有一方要先打破僵局，先随便整一个值出来，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终就会收敛到一个解。

EM解高斯混合模型

  在我们上面这个问题里面，我们是先随便猜一下男生（身高）的正态分布的参数：如均值和方差是多少。例如男生的均值是1米7，方差是0.1米（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（lz某个身高值代入男生和女生的高斯分布中，选择概率大的作为其所在分布），这个是属于Expectation一步。

  有了每个人的归属，已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。

  然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。

  这里把每个人（样本）的完整描述看做是三元组yi={xi,zi1,zi2}，其中，xi是第i个样本的观测值，对应身高，可观测值。zi1和zi2表示男生和女生这两个高斯分布中哪个被用来产生值xi，就是说这两个值标记这个人到底是男生还是女生（的身高分布产生的）。这两个值我们是不知道的，是隐含变量。确切的说，zij在xi由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果zi1和zi2的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此我们只能用EM算法。

   假设已经知道这个隐含变量了，那么直接按上面说的最大似然估计求解那个分布的参数就好了。我们可以先给这个分布弄一个初始值，然后求这个隐含变量的期望，当成是这个隐含变量的已知值，那么现在就可以用最大似然求解那个分布的参数了吧，那假设这个参数比之前的那个随机的参数要好，它更能表达真实的分布，那么我们再通过这个参数确定的分布去求这个隐含变量的期望，然后再最大化，得到另一个更优的参数，……迭代，就能得到一个皆大欢喜的结果了。

连续隐变量模型

主成分分析-PCA

PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

• 应用：
数据压缩
数据可视化：通过将数据投影到前两个主体上。
特征提取
维度减少

•算法：找到D维数据的M个主要成分
–选择S的前M个特征向量（数据协方差矩阵）：
–将每个输入向量x投影到该子空间中

强化学习

Q-leanring

QLearning是强化学习算法中value-based的算法，Q即为Q（s,a）就是在某一时刻的 s 状态下(s∈S)，采取动作a (a∈A)动作能够获得收益的期望，环境会根据agent的动作反馈相应的回报reward r，所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值，然后根据Q值来选取能够获得最大的收益的动作。

Step 1 给定参数γ和reward矩阵R。
Step 2 令Q := 0。 # 将表格Q初始化为0
Step 3 For each episode:
　　3.1 随机选择一个初始的状态s。
　　3.2 若未达到目标状态，则执行以下几步
　　　　(1) 在当前状态s的所有行为中选取一个行为a.
　　　　(2) 利用选定的行为a, 得到下一个状态~s.
　　　　(3) 按照(1.1)计算Q(s, a)
　　　　(4) 令s := ~s

　　Agent利用上述算法从经验中进行学习。每一个episode相当于training session。在一个training session中，agent探索外界环境，并接收外界环境的reward, 直到达到目标状态。训练的目的是要强化agent的“大脑”（用Q表示）。训练得越多，则Q被优化得更好。当矩阵Q被训练强化后，agent便很容易找到目标状态得最快路径了。

s是状态
ε-greedy 表示决策策略，例如ε-greedy=0.9表示90%按照Q表最优值选择行为，10%随机选择行为
α是学习效率，表示这次误差有多少要去学习，小于1。
γ是对未来奖励的衰减值

MDP的作用是为了简化模型，贝尔曼方程的引用是为了呈现t时刻与t+1时刻的价值函数的关系

马尔可夫过程

马尔科夫过程：马尔科夫过程是随机过程的一种，随机过程是对一连串随机变量(或事件)变迁或者说动态关系的描述，而马尔科夫过程就是满足马尔科夫性的随机过程，它由二元组M= (S,P)组成，且满足：S是有限状态集合， P是状态转移概率。整个状态与状态之间的转换过程即为马尔科夫过程。

马尔可夫决策过程

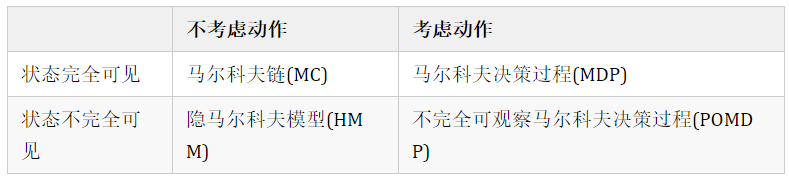
S：表示状态集（states）
A：表示一组动作（actions）
P：表示状态转移概率.a表示在当前sES状态下，经过aEA作用后，会转移到的其他状态的概率分布情况
R：奖励函数（reward function）表示agent采取某个动作后的即时奖励46.2

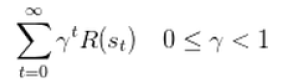
y：折扣系数意味着当下的reward比未来反馈的reward更重要
1.智能体初始状态为S0
2.选择一个动作a0
3.按概率转移矩阵Psa转移到了下一个状态S1然后。。。

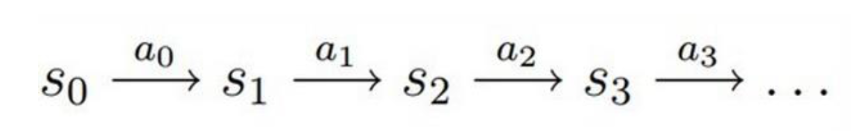
状态价值函数：

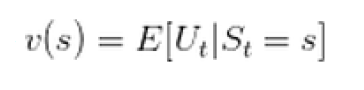
t时刻的状态s能获得的未来回报的期望价值函数用来衡量某一状态或状态-动作对的优劣价，累计奖励的期望最优价值函数：所有策略下的最优累计奖励期望

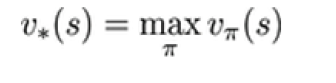
策略：已知状态下可能产生动作的概率分布

马尔可夫奖励过程

马尔可夫奖励过程就是含有奖励的马尔可夫链，要想理解MRP方程的含义，我们就得弄清楚奖励函数的由来，我们可以把奖励表述为进入某一状态后收获的奖励。奖励函数如下所示：

贝尔曼方程

Bellman方程：当前状态的价值和下一步的价值及当前的奖励（Reward）有关
价值函数分解为当前的奖励和下一步的价值两部分